Плач математика

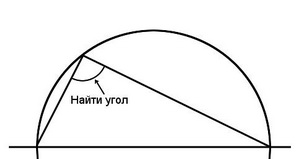Сразу несколько читателей прислали мне ссылку на замечательную статью астронавта Пола Локхарда "Плач математика". Прочесть статью (очень рекомендую прочесть) можно здесь:

Краткий пересказ основных тезисов статьи для тех, кому лень читать.

1. Школьные преподаватели математики — хищные упыри, целенаправленно убивающие в детях интерес к математике.
2. Преподавать математику в традиционном виде — в виде формул и определений — это не более разумно, чем учить детей плаванию, не подпуская их к бассейну.
3. Соответственно, "отличник", который лучше других детей сможет перечислить наизусть важные для пловца мышцы, с большой долей вероятности не сумеет проплыть самостоятельно даже от одного бортика бассейна до другого.
4. Современная система преподавания математики прогнила до такой степени, что не "заостряет" ум, как лгут нам чиновники от образования, а "затупляет" его. Проще говоря, если вы хотите, чтобы ваш ребёнок хорошо разбирался в математике, самое разумное — сделать ему под каким-нибудь предлогом освобождение от школьных математических уроков.
5. Суть математики — в игре и в поиске. Доказать, например, теорему Пифагора — весьма и весьма увлекательный квест для ребёнка. Проблема только в том, что на уроках дети не решают задачи, а всего лишь заучивают наизусть чужие решения, изложенные при этом заумным (даже для взрослого математика) языком.

Теперь мои комментарии к этому эссе.

Во-первых, хочу сказать спасибо fregimus за перевод.

Во-вторых, хочу сослаться на мой собственный пост "Кибершкола", где я рассказываю об альтернативе современной школе.

И, в-третьих, хочу продолжить эссе Локхарда кратким планом: как бы учил детей математике я. (Возможно, кстати, некоторые жители Петербурга догадаются сейчас, где мне повезло познакомиться на практике с этой замечательной системой).

Так вот. Каждый мой урок начинался бы одинаково. Я бы выписывал на доску задачи на сегодня. Допустим, три задачи обычных, две задачи повышенной сложности и одну — совсем сложную. Решение каждой задачи оценивалось бы в определённое количество очков.

Объяснив детям суть задач и ответив на их вопросы, я бы... отпускал детей заниматься своими делами.

В следующий час я бы разбирал с оставшимися на уроке детьми старые задачи, которые были заданы пару недель назад, и которые большинство детей уже решило или не захотело решать. Этот разбор, повторюсь, был бы необязательным. Кто хочет — слушает, кто не хочет — занимается чем хочет.

И, наконец, дальше, в течение всего дня, своими делами занимался бы уже я. Каждый ученик при этом мог бы подойти ко мне и сдать решённую им задачу, получив за это оговоренные очки. Разумеется, "сдать задачу" означало бы не просто сказать ответ, а ещё и объяснить бы мне (на словах) решение и ответить на мои каверзные вопросы.

Набранные детьми очки суммировались бы, и раз в месяц набравшие наибольшее количество баллов премировались бы разными плюшками. Например, поездками на городскую математическую олимпиаду.

Детям, которые задач решали бы мало, я бы предлагал перейти к другому преподавателю, который давал бы более лёгкие задачи. Детей же талантливых, которые щёлкали бы мои задачи как орешки, я бы, наоборот, отправлял в более продвинутые группы. Наверное, излишне говорить, что все группы были бы разновозрастными.

Как итог, по окончанию школы мы получали бы большое количество знающих и любящих математику подростков, а также большое количество подростков, которые, зная математику на весьма посредственном уровне, сохраняли бы в себе живой интерес к знаниям и спокойное отношение к разного рода формулам.

© Фриц Моисеевич Морген