Когда педагогам никто не мешает

Наблюдал вчера любопытную сцену: взрослая женщина в больнице занималась вместе с ребёнком математикой. Дама зачитывала мальчику учебник, а школьник с серьёзным и сосредоточенным лицом что-то записывал на листке в клеточку.

«Сколько раз можно уложить… У-ЛО-ЖИТЬ… отрезок о-бэ… ОТ-РЕ-ЗОК О-БЭ… в длине отрезка ОА… В ДЛИ-НЕ… В ДЛИ-НЕ… ОТ-РЕЗ-КА… О-А…»

Лично я всегда терпеть не мог скорбных на голову людей, которые думают, будто «сказать понятнее» — это значит «сказать погромче, эдаким мерзким назидательным голосом». Мне сразу же стало жалко несчастного ребёнка. И сразу же я подумал про тригонометрию.

Дело в том, что в школе я тригонометрии не понимал вообще. Для меня синусы и тангенсы всегда были полностью оторванными от реальности функциями, не имеющими никакой связи с геометрией. Конечно, я мог подставить одну формулу в другую и решить «задачу», но я и близко не мог объяснить, скажем, что такое косинус и как можно грубо прикинуть его значение. Разного рода мишенеобразные круги, которые учитель рисовал на доске, я банально игнорировал, равно как и заклинания типа «угол пи-пополам».

Помните тысячи историй про «глупых американцев», которые неправильно умножали цифры на калькуляторе и давали с десяти долларов девяносто долларов сдачи? Вот в тригонометрии подобным «американцем» был я — у меня не было и тени понимания смысла происходящего, из-за чего становился заложником выведенных кем-то до меня формул.

Однако несколько дней назад я очередной раз наткнулся на слово «синус». Залез по привычке в Вики, чтобы, наконец, разобраться с этим понятием и… был поражён открывшейся передо мной картиной.

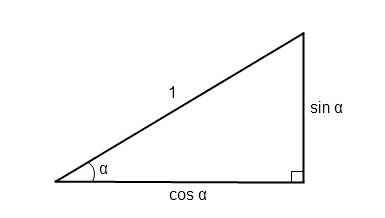
Оказывается, всё что надо — это тупо нарисовать прямоугольный треугольник с гипотенузой длиной в единицу. В этом треугольнике синусом будет дальний катет, а косинусом — ближний катет. Вот и вся тригонометрическая премудрость. Собственно, даже слово тригонометрия расшифровывается как «тригон + метр» — измерение треугольников.

Разумеется, есть ещё тангенсы и котангенсы, есть градусы и радианы, есть сферическая тригонометрия и разные прочие непотребства. Но вот этого простого треугольника с синусом и косинусом более чем достаточно, чтобы неживые формулы насытились реальным смыслом. И чтобы я понял, что синус нуля — это ноль, а синус 90 градусов — единица.

Почему за всё время школьного и институтского обучения у меня не нашлось пяти минут, чтобы разобраться в этих элементарных для понимания терминах?

Полагаю, корень зла надо искать именно в том методе школьного преподавания, с которого я начал сегодняшний пост. С «отрезка ОВ», который ребёнку следовало уложить нужное число раз в «отрезке ОА». Пол Локхард очень верно сказал в своём плаче математика: бессмысленный педантичный формализм убивает интерес к математике на корню.

Из любытства я сейчас заглянул в «официальное» определение синуса:

«Если M(t) — точка числовой окружности, соответствующая числу t, то ординату точки M называют синусом числа t и обозначают sin t».

Ничуть не удивляюсь, что в школе у меня не возникло желания тратить время на расшифровку подобной ереси.

Кстати, я далёк от мысли произносить матерные слова в адрес авторов учебников. Думаю, они просто не могут себе позволить писать понятно. Дело в том, что «понятно» — это практически всегда «неточно». А у учебника по математике с неточностями особых шансов пройти цензуру нет. Вот и появляется у нас в определении птичьеязычная «ордината» вместо понятной школьнику «оси y».

Впрочем, заумность — это только половина проблемы. Вторая половина беды — «задачи на закрепление», из которых чуть менее чем полностью школьный курс математики и состоит.

Помните длиннобородый анекдот про Штрилица?

«Идёт психологическое тестирование нацистов. Вызывают первого.
— Задумайте двузначное число.
— Двадцать три.
— А может, тридцать два?
— Может, и тридцать два.
Пишут в личном деле: характер слабый, неуверенный. Зовут следующего.
— Задумайте двузначное число.
— Пятьдесят семь.
— А может, семьдесят пять?
— Нет, пятьдесят семь.
Пишут в личном деле: характер стойкий, нордический. Зовут ещё одного.
— Задумайте двузначное число.
— Сорок четыре.
— Штирлиц! Не мешайте работать!»

А теперь типичное задание из учебника:

«Придумайте ещё десять аналогичных анекдотов со своими цифрами, в которых вместо Штрилица фигурируют Вовочка, Чапаев, чукча и другие комические персонажи. Пример:

"Идёт психологическое тестирование гусар. Вызывают первого.
— Задумайте двузначное число.
— Шестьдесят восемь.
— А может, восемьдесят шесть?…"»

Как считаете, будет школьник до колик в животе смеяться во время выполнения этого задания? Сильно сомневаюсь. Анекдоты, как и осетрина, бывают только первой свежести.

Ровно то же самое можно сказать и о математических задачах. Переписывать по десять раз уже единожды решённую кем-то задачу — удовольствие, мягко говоря, не для всех. Как минимум, не для детей с математическим складом ума. Задача по-настоящему интересна только в том случае, если ты находишь её решение сам.

Приведу пример из темы синусов и косинусов. Можно без труда самостоятельно вычислить синус 45 и синус 30 градусов, просто нарисовав соответствующие треугольники и немного задумавшись над ними. Теорема Пифагора плюс минимальная смекалка — и мы повторяем подвиг математиков древности, и с радостью убеждаемся, что найденное нами значение соответствует цифре в справочнике.

Но вот что-то я ни разу не помню, чтобы в школе давали подобные задачи. В школе всегда сначала объясняют готовое решение, а потом заставляют детей это готовое решение выучить. Решать что-либо самостоятельно в школе, насколько я помню, не нужно вообще.

Короче, подведу итог. Школьная математика имеет не больше отношения к математике, чем апельсиновая кожура к целому апельсину. И если есть выбор — дать детям кожуру (точные определения) или дать детям мякоть (задачи) — делать выбор в пользу кожуры будет только бесконечно далёкий от понимания сути знаний человек.

Напоследок, короткая история из жизни.

Какое-то время назад я вступил в дискуссию с одной знакомой на предмет полезности школ. В ходе спора со стороны моего оппонента прозвучал следующий аргумент:

«Девочки, в среднем, учатся лучше, чем мальчики. И после школы женщины, в среднем, умнее мужчин. Если бы оценки в школе ничего не значили, было бы наоборот».

Я, к стыду своему, про эту статистику раньше не знал. Ну, то есть, что среди девочек больше отличниц — я догадывался. Но вот то, что средняя женщина умнее среднего мужчины я, грешным делом, даже не подозревал. Полагаю, многие захотят с этим поспорить.

Впрочем, после некоторого размышления, мне пришёл в голову более наглядный способ измерения эффективности работы профессиональных педагогов.

Большинство детей учится как в школе, так и за её пределами. Разделить школьные знания и знания, полученные от родителей, довольно тяжело.

Поэтому, чтобы наше сравнение было корректным, надо сравнивать детей, которые никогда не учились в школе, и детей, которые никогда не учились за пределами школы. То есть, надо сравнивать успехи хоумскулеров и успехи детдомовцев.

Как полагаете, коллеги, в чью пользу будет это сравнение?

© Фриц Моисеевич Морген